Logga in
Andelar





| | 8 sidor teori |
| | 56 Uppgifter - Nivå 1 - 3 |
| | Varje lektion är menad motsvara 1-2 lektioner i klassrummet. |
- Andel
- Andel, delen och det hela
- Proportionalitet
Förkunskaper
Andel
En andel beskriver hur mycket det finns av något i förhållande till det totala. Det är alltid ett jämförelsetal, som hälften
eller 50 %
, och inte ett absolut värde som 25kr
eller 42kg
. En andel kan t.ex. anges som ett bråk, ett decimaltal eller i procent.
| Andel | Bråk | Decimaltal | Procent |
|---|---|---|---|
| En hundradel | 1/100 | 0,01 | 1 % |
| Tre åttondelar | 3/8 | 0,375 | 37,5 % |
| Två femtedelar | \dfrac 2 5 | 0,4 | 40 % |
| Tre fjärdedelar | \dfrac 3 4 | 0,75 | 75 % |
Andel, delen och det hela
För att beräkna hur stor andel som en del (t.ex. 15 st. tjejer) utgör av det hela (exempelvis en klass på 30 elever), beräknar man kvoten enligt andelsformeln.
Andelen=Delen/Det hela
Proportionalitet
Två storheter är proportionella om de förändras i samma takt. Det betyder att om den ena storheten ökar eller minskar, så gör den andra det också — med en konstant faktor.

Om det kostar 40 kronor för 1 timmes cykelhyra, kostar det 80 kronor för 2 timmar och 120 kronor för 3 timmar. Kostnaden per timme är alltid 40 kronor. Eftersom priset ökar linjärt med tiden, är kostnaden proportionell mot hyrestiden. I en graf representeras proportionalitet av en rät linje som går genom origo. Om hyrestiden markeras på x-axeln och kostnaden på y-axeln, bildar punkterna en rät linje från (0,0).

Proportionalitet innebär också att förhållandet mellan de två storheterna alltid är konstant.
120kr/3h=80kr/2=40kr/1h=40.kr /h.Vad är andelen?
Ledtråd
Använd andelsformeln.
Lösning
Det hela. Vi använder andelsformeln för att beräkna andelen. Vi förkortar bråket så långt som möjligt och kan börja med att förkorta med 2 eftersom både täljare och nämnare är jämna tal. Du jobbar alltså 1/4 av veckan.
Vad är delen?
Ledtråd
Använd andelsformeln.
Lösning
Andelen= 0,8 och Det hela= 2
VL * 2=HL* 2
Omarrangera ekvation
Vad är det hela?
Ledtråd
Använd andelsformeln.
Lösning
Andelen= 0,1 och Delen= 7
VL * Det hela=HL* Det hela
VL * 10=HL* 10
Gödselblandning och proportionalitet
Bönder blandar ofta gödsel med vatten i förhållande 100:10, vilket innebär att 100 gram gödsel blandas med 10 liter vatten.
Ledtråd
Lösning
100g/10L=10.g /L.
Detta betyder att 1 liter vatten används per 10 gram gödsel. Beräkna nu förhållandena i Elias och Julias blandningar för att kontrollera om de följer samma proportion.
Elias& &Julia 250/20=12,5.g /L. & & 25/2=12,5.g /L.
Eftersom både Elias och Julia har samma förhållandevärde på 12,5.g /L., är deras blandningar proportionella mot varandra. Däremot skiljer sig deras förhållande från böndernas, vilket innebär att deras blandningar inte är proportionella mot den som vanligtvis används av bönder.
400/10=40 liter
Detta innebär att Elias och Julia behöver 40 liter vatten för att bibehålla samma proportion.
I ett bråk beskriver nämnaren det hela
. Förlänger vi 1941 så att nämnaren ligger över 100 men så nära 100 som möjligt, kan vi läsa av det minsta antalet killar på skolan i täljaren. Skillnaden mellan nämnaren och täljaren blir det minsta antalet tjejer på skolan.
Hitta minsta möjliga nämnare över 100
För att hitta den minsta möjliga nämnaren över 100 multiplicerar vi med så små heltal som möjligt tills nämnaren når över 100. Vi börjar med 2.
Nämnaren blev inte större än 100 så vi måste förlänga bråket med något annat tal större än 2. Vi testar nästa heltal: 3.
Nu hamnade nämnaren över 100. Då vet vi att det går minst 123 elever på skolan och 57 av dessa är pojkar. Då måste det minsta antalet flickor på skolan vara 123-57=66 st.
De blå fälten (18 st.) i nedanstående lyckohjul är lika stora och de vita fälten (18 st.) är lika stora. Hur stor medelpunktsvinkel har varje blått fält om de tillsammans utgör 70 % av hjulets totala area?

De 36 fälten bildar tillsammans ett helt varv (360^(∘)), och eftersom 70 % av lyckohjulet är blått måste även de blå fälten utgöra 70 % av ett helt varv, dvs. 360^(∘) * 0,7 = 252^(∘). Om de 18 blå fälten tillsammans utgör 252^(∘) av cirkeln, och är lika stora, måste varje enskilt fält ha medelpunktsvinkeln 252^(∘)/18=14^(∘).
Svetlana jobbar som konditor och ska baka tre sorters kakor: drömmar, hallongrottor och havreflarn. Andelen drömmar är 13 och andelen hallongrottor är 37.
Om vi lägger ihop andelen drömmar, hallongrottor och havreflarn ska summan bli 1 eftersom det är alla kakor. Vi vet inte vad andelen havreflarn är, så vi kallar den x och löser sedan ut den ur ekvationen.
Andelen havreflarn är 521.
Vi skriver om andelarna så att alla har nämnaren 21. Då är det lättare att avgöra vilken som det finns flest av.
| Kakor | Andel | Förläng med | = |
|---|---|---|---|
| Drömmar | 1/3 | 7 | 7/21 |
| Hallongrottor | 3/7 | 3 | 9/21 |
| Havreflarn | 5/21 | - | 5/21 |
Eftersom alla har samma nämnare kan vi läsa av att 921 är den största andelen, då den har den största täljaren. Vi vet då att det finns 18 stycken hallongrottor och att detta utgör 37 av alla kakor. Om vi antar att det totala antalet kakor är x får vi en ekvation som vi kan lösa.
Det finns totalt 42 kakor.
En kanna innehåller saftkoncentrat. På saftförpackningen står det att man ska blanda saft och vatten enligt 1+4 för att smaken ska bli bra.
Eftersom 1 del utgör saft och 4 delar är vatten kan totala mängden saft skrivas som 1+4=5 delar. Andelen vatten blir därför
Volym vatten/Volym blandad saft=4/5.
Vi har 1,5 liter saft, vilket utgör Det hela
. Vi sätter in våra värden i andelsformeln och löser ut "Delen", som ju var mängden vatten.
Man har alltså använt 1,2 liter (eller 12dl) vatten till saften.
Vi tar reda på hur mycket saft man kan blanda med 60cl koncentrat. Fördelningen 1+4 betyder att mängden vatten är fyra gånger större än mängden koncentrat. Det betyder att man ska tillsätta
4*60=240cl
vatten. Totalt ger det 60+240=300cl saftblanding. 300cl är lika med 3 liter, så koncentratet räcker för att göra bålen.
Vi bestämmer heltidslönen under en vecka genom att multiplicera timlönen med antalet timmar: 140* 40=5 600 kr. Vi vet att övertidslönen utgör andelen 75 av heltidslönen, som är det hela. Vi räknar nu ut hur mycket Henrik tjänade på sina övertidstimmar, dvs. delen, genom att sätta in det vi vet i andelsformeln.
Övertidslönen var alltså 7 840kr. Totalt under veckan tjänade han därför 5 600 + 7 840 = 13 440 kr.
Vi skriver ner det vi vet. Eftersom Lorenzo hade druckit upp tre fjärdedelar har han en fjärdedel kvar.
| Lorenzo | Omar | |
|---|---|---|
| Andel | 1/4 | 1/2 |
| Delen | x | x+1 |
| Hela flaskan | ? | 10 dl |
Vi börjar med att ta reda på vad x är genom att använda andelsformeln för Omars flaska. Vi skriver en halv som 0,5 för enkelhetens skull.
Omars flaska
Nu vet vi att x=4dl och vi har då tillräckligt med information för att ta reda på volymen av Lorenzos flaska.
| Lorenzo | Omar | |
|---|---|---|
| Andel | 1/4 | 1/2 |
| Delen | 4dl | 5dl |
| Hela flaskan | y | 10dl |
Lorenzos flaska
Lorenzos flaska är alltså ganska stor. Den rymmer 1,6 liter.
I nedanstående tabell ser du hur mycket inkomstskatt två kommuner får in under en månad. Genomsnittslönen är 25 000 kr i båda kommuner.
| Kommun | Sysselsatta | Total skatt |
|---|---|---|
| A | 1 403 | 10 522 500 kr |
| B | 10 901 | 95 383 750 kr |
Vi beräknar skattesatsen för varje kommun separat och jämför dem sedan.
Kommun A
Vi börjar med att beräkna den totala lönen, eller det hela
, för alla sysselsatta i kommunen. Eftersom genomsnittslönen är 25 000kr multiplicerar vi detta med antalet arbetande i kommunen.
I kommun A tjänar de sysselsatta 35 075 000kr per månad. Av detta betalas 10 522 500kr som skatt. Vi beräknar hur stor andel det är.
I kommun A är alltså skattesatsen 30 %.
Kommun B
Vi gör på samma sätt och multiplicerar genomsnittslönen med antalet sysselsatta i kommunen.
I kommun B tjänar de sysselsatta 272 525 000kr per månad. Nu beräknar vi hur stor del skatten utgör av detta.
I kommun A är skattesatsen 30 % och i kommun B 35 %, så kommun B har högst skatt.
För att kommunerna ska ha samma skattesats måste kommun A höja sin till 35 %. I förra deluppgiften beräknade vi att man totalt tjänade 35 075 000kr i kommunen. Det betyder att den totala skatten blir
35 075 000* 0,35=12 276 250kr
När Pelle fick 1,5 % i löneökning blev det 300kr. Hur många kronor skulle han ha fått i löneökning om löneökningen hade varit 4 %?
Vi kan börja med att beräkna hur mycket 1 % löneökning hade motsvarat. Eftersom 300kr är 1,5 % kan vi göra det genom att dividera 300 med 1,5
1 % motsvaras alltså av 200kr. Men vi skulle ju beräkna hur mycket 4 % motsvarar. Vi multiplicerar därför med 4: 200*4=800. Om Pelle hade fått 4 % löneökning hade han alltså fått 800kr.
25 av ett tal är 1. Vilket är talet?
Vi vet att andelen 25 av ett tal, som vi kan kalla x, ska vara lika med 1. Talet x är alltså det hela och 1 är den del av det hela som utgör 25. Vi använder andelsformeln för att bestämma x.
Talet är alltså 2,5.
Vi gör en tabell som beskriver de två lånen.
| Person | Lånebelopp | Räntesats | Årsränta |
|---|---|---|---|
| Anders | 50 000 kr | 4.2 % | ? |
| Stina | ? | 7.2 % | ? |
| Årlig räntekostnad | 9300 kr |
För att beräkna årsräntan för Anders lån multiplicerar vi lånebeloppet med räntesatsen i decimalform: 50 000 kr * 0.042=2100 kr. Nu kan vi direkt räkna ut Stinas räntekostnad som är den totala räntekostnaden minus räntekostnaden för Anders lån: 9300 kr - 2100 kr =7200 kr. Stinas räntekostnad är alltså 7200 kr. Delar vi årsräntan (Delen) med räntesatsen (Andelen) kan vi bestämma lånebeloppet (Det hela). 7.2 % kan vi skriva som 0.072.
Stinas lånebelopp är på 100 000 kr. Nu fyller vi i resten av tabellen.
| Person | Lånebelopp | Räntesats | Årsränta |
|---|---|---|---|
| Anders | 50 000 kr | 4.2 % | 2100 kr |
| Stina | 100 000 kr | 7.2 % | 7200 kr |
| Årlig räntekostnad | 9300 kr |
Stinas räntekostnad är alltså 7200 kr och hennes lånebelopp är 100 000 kr.
Tabellen visar hur konsumentprisindex har utvecklats under tidsperioden 2011-2015.
| År | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|
| Index | 311.4 | 314.2 | 314.1 | 313.5 | 313.4 |
Vi vet vad Angelica betalade i månadshyra år 2015 och ska bestämma vad hyran borde ha varit år 2011 om hyresnivån utvecklats på samma sätt som KPI. Vi kan skriva följande samband (FF anger förändringsfaktorn):
Hyra_(2011) * FF = Hyra_(2015). Månadshyran 2011 kan vi kalla x och förändringsfaktorn för KPI beräknas genom att dividera 313.4 med 311.4. Detta ger oss x * 313.4/311.4 = 3700. Vi löser ut x ur ekvationen.
Hyran år 2011 borde ha varit ungefär 3676 kr/månad.
Vi vet att fem fakturor har varit försenade. Om varje försening ger 150 kr i förseningsavgift har Kalle totalt betalat 150* 5=750 kr i avgifter. Av den totala kostnaden har alltså11 250-750=10 500 krvarit räntekostnad och detta ska alltså vara 7 % av det lånade beloppet. Vi sätter in dessa värden i andelsformeln.
Lånet var på 150 000 kr.
Följande skylt finns i en affär:
Hur stor är rabatten i procent?
För att bestämma hur stor rabatten är måste vi först beräkna hur mycket det kostar att köpa de tre varorna till ordinarie pris. Från skylten ser vi att ordinarie pris för en vara är 12.90 kr så tre varor måste då kosta 3* 12.90=38.70 kr. Enligt samma skylt kan man köpa dessa tre varor för 30 kr. Genom att använda andelsformeln beräknar vi hur många procent det rabatterade priset utgör av det ordinarie.
Andelen är 0.78 vilket innebär att det lägre priset utgör 78 % av det ordinarie. Rabatten är skillnaden mellan 78 % och 100 %, dvs. 100 % - 78 % = 22 %.
Linus har sett reklam för ett sms-lån och vill jämföra det med ett lån på en bank
Från uppgiften vet vi att bankens årsränta är 5.6 %. Genom att multiplicera lånets storlek med räntan uttryckt i decimalform, dvs. 0.056, så kan vi bestämma årsräntan i kronor som du måste betala till banken. 3000* 0.056=168 kr.
Kostnaden per månad om man inte betalar tillbaka sms-lånet är alltså 375 kr och om man struntar i att betala tillbaka lånet på ett helt år kommer den totala avgiften man är skyldig att vara 375 * 12=4500 kr. Nu använder vi andelsformeln för att bestämma hur stor andel avgiften utgör av det lånade beloppet.
Du ska alltså betala tillbaka 150 % av lånebeloppet efter ett år vilket är årsräntan för sms-lånet.
Martin och Johanna ska köpa en ny bil. Johanna fastnar för en bil som kostar 194 000 kr. Martin påstår att värdet på denna sorts bil sjunker med ungefär 17 % per år. De funderar på hur mycket den bilen skulle vara värd om 3 år och var och en beräknar på sitt sätt. Vem har rätt? Motivera ditt svar.
När något förändras med en konstant procentsats så kan detta beskrivas med en exponentialfunktion, dvs. en funktion som står på formen y = C * a^x, där C är startvärde och a är en förändringsfaktor. Nu kan vi titta på Martins och Johannas beräkning.
Martins beräkning
Martin har resonerat att om man adderar 17 % tre gånger så får man den totala värdeminskningen efter tre år. Men denna modell innebär att den procentuella minskningen för varje år räknas på bilens ursprungspris vilket inte stämmer överens med hur en exponentialfunktion funkar.
Johannas beräkning
Johanna börjar med att bestämma den förändringsfaktor som en värdeminskning på 17 % motsvarar, dvs. 1-0.17=0.83 Genom att multiplicera denna förändringsfaktor med bilens ursprungliga pris tre gånger får vi värdet efter tre år, dvs. 0.83^3* 194 000 kr=110 927 kr. Johanna har alltså gjort rätt.
En affär sänkte priset på jeans först med 25 % och därefter med ytterligare 25 %. Peter påstår att priset då hade sänkts med totalt 50 %. Har Peter rätt? Motivera ditt svar.
Som ett räkneexempel kan vi utgå från att ett par jeans ursprungligen kostade 400 kr. När ett pris sänks med 25 % är förändringsfaktorn 0.75. Det nya priset blir därför 400 * 0.75 = 300 kr. Om man sänker priset med 25 % igen ska förändringsfaktorn multipliceras med det redan sänkta priset. Det nya priset blir då 300 * 0.75 = 225 kr. Om det hade varit som Peter påstår hade det nya priset varit hälften av 400 kr dvs. 200 kr, men det blev ju 225 kr. Peter har därför inte rätt.
Hur stor del av rektangeln är skuggad?

1/2 3/4 3/7 2/8 3/8
Det finns två skuggade områden i rektangeln. Vi delar upp rektangeln i två för att räkna ut varje skugga.
Övre rektangeln
Vi drar en diagonal så att vi får fyra likadana trianglar.
Totalt blir det fyra trianglar och en är skuggad. Andelen som är skuggad av den övre rektangeln är då 14. Eftersom den övre rektangeln är hälften av hela rektangeln måste vi dela detta på 2.
Skuggan i den övre rektangeln är alltså 18 av hela rektangeln.
Undre rektangeln
Diagonalen genom rektangeln delar den i två lika stora delar.
Det betyder att den skuggade delen kommer vara hälften av den undre rektangeln, dvs 12. Precis som i den övre rektangeln måste vi dela andelen på 2. Skuggan i den undre rektangeln blir då 1/22= 14 av hela rektangeln.
Hela rektangeln
Lägger vi ihop andelen som är skuggad i övre och undre rektangeln får vi andelen som är skuggan i hela rektangeln.
Delen av rektangeln som är skuggad är alltså 38.
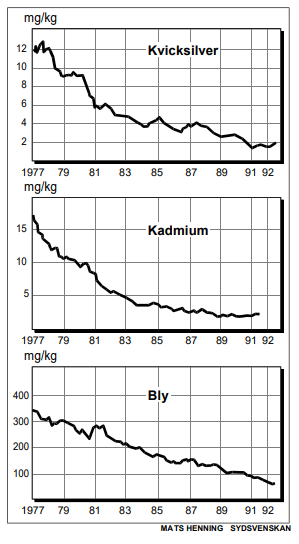
I en tidningsartikel med rubriken ”Allt mindre gift i rötslam” fanns följande diagram. Där visas halterna av några giftiga ämnen i rötslam från kommunala reningsverk.
Besvara följande frågor med hjälp av diagrammen ovan.
Hur många procent sjönk blyhalten i rötslammet mellan år 1979 och 1991?
År 1989 kom 230 000 ton rötslam från reningsverken. Hur mycket kvicksilver fanns det totalt i rötslammet?
För att kunna ta reda på hur många procent blyhalten sjönk med så måste vi ta reda på vilka värden som fanns vid årtalen. Vid år 1979 var blyhalten 300 mg/kg, och vid 1991 hade den minskat till cirka 90 mg/kg. Vi behöver som nästa steg beräkna hur stor andel 90 mg/kg är av 300 mg/kg.
90 mg/kg är alltså 30 % av 300 mg/kg. Denna minskning av blyhalten var därmed på 100 % - 30 % = 70 %.
Vi behöver nu först rådfråga diagrammen för att ta reda på hur stor kvicksilverhalten var år 1989. Vi hittar då en halt på cirka 3 mg/kg. Halten kvicksilver är uttryckt i enheten mg/kg, medan mängden rötslam är uttryckt i ton, vilket inte går ihop. Vi väljer att omvandla mängden rötslam till kg: 230 000ton = 230 000 000kg. Vi kan nu multiplicera mängden rötslam med kvicksilverhalten för att hitta mängden kvicksilver: 3 * 230 000 000 = 690 000 000. Enheten på detta blir alltså mg. Vi bör nu omvandla från enheten mg till något mer lämpligt, för att slippa alla dessa nollor. 690 000 000mg = 690 000g = 690kg Det fanns alltså cirka 690 kg kvicksilver i rötslammet år 1989.
Peter och Karin ska köpa en begagnad bil. Karin fastnar för en fransk bil som kostar 114 000 kr. Peter påstår att värdet på denna sorts bil sjunker med ungefär 11 % per år. Peter och Karin funderar på hur mycket den bilen skulle vara värd om 3 år och var och en beräknar på sitt sätt.
Vem har tolkat problemet rätt? Motivera genom att beskriva hur Peter och Karin kan ha resonerat.
Vi börjar med att tolka problemet själva. För att kunna räkna ut värdet efter 3 år måste vi räkna ut förändringsfaktorn. Den får genom att göra om 11 % till decimalform och dra bort det från 1, eftersom värdet sjunker. 1-0.11=0.89 Nu vill vi multiplicera förändringsfaktorn med bilens pris för att få värdet efter 3 år. Vi måste därför göra multiplikationen 3 gånger och istället för att upprepa multiplikationen kan vi skriva talet som en potens. 0.89^3 * 114 000 Vi har nu ett uttryck för bilens värde efter 3 år och ser att Karin har gjort likadant. Det betyder att Peter har gjort något fel. Eftersom det minskar med 11 % varje år tänker Peter att han ska multiplicera med 3. Han räknar ut förändringsfaktorn och får den till 0.67 vilket betyder att priset sjunker med 33 %. Peter räknar alltså ut att bilens värde sjunker en gång med 33 % istället för 3 gånger med 11 % per gång.