Logga in
Slumpförsök i flera steg





| | 9 sidor teori |
| | 34 Uppgifter - Nivå 1 - 3 |
| | Varje lektion är menad motsvara 1-2 lektioner i klassrummet. |
- Oberoende händelser
- Beroende händelser
- Multiplikation av sannolikheter
- Addition av sannolikheter
- Träddiagram
- Utfallsmatris
Förkunskaper
Oberoende händelser
Två händelser A och B är oberoende om den ena händelsens förekomst inte påverkar den andra. De är också oberoende om och endast om sannolikheten att båda inträffar är lika med produkten av deras individuella sannolikheter.
Förklaring
Till exempel — tänk dig att en skål innehåller tre kulor: en grön, en orange och en blå. Låt G, B och O vara händelserna att dra den gröna, blå och orange kulan, respektive.

Anta att man drar en kula i taget, och att den första kulan läggs tillbaka innan den andra dragningen. Vad är sannolikheten att först dra en grön kula och sedan en orange kula?

I det här fallet finns det 9 möjliga utfall när man drar två kulor, en i taget, och lägger tillbaka den första innan nästa dragning. Bara 1 av dessa utfall motsvarar händelsen att först dra en grön kula och sedan en orange kula.
G G G B G O B B B G B O O O O G O B
Därför är sannolikheten att först dra en grön kula och sedan en orange kula 1/9.
P(först G och sedan O)= 1/9
Nästa steg är att beräkna sannolikheten för varje händelse var för sig. Sannolikheten att först dra en grön kula får man genom att dela antalet gynnsamma utfall med det totala antalet kulor. Skålen innehåller 3 kulor, varav 1 är grön. Eftersom kulan läggs tillbaka, finns det vid nästa dragning återigen 3 kulor i skålen, varav 1 är orange.
P( G)= 1/3 P( O)= 1/3
Eftersom sannolikheten att båda händelserna inträffar är lika med produkten av deras individuella sannolikheter, är händelserna oberoende.
P(först G och sedan O) & = & P( G) & * & P( O) [0.3em] 1/9 & = & 1/3 & * & 1/3 [0.3em]
Beroende händelser
Två händelser A och B kallas beroende om det att den ena inträffar påverkar sannolikheten för att den andra inträffar. Om händelserna är beroende, är sannolikheten att båda inträffar lika med produkten av sannolikheten att den första händelsen inträffar och sannolikheten att den andra händelsen inträffar efter att den första redan har hänt.
Förklaring
Till exempel — anta att en skål innehåller tre kulor: en grön, en orange och en blå. Låt G, B och O vara händelserna att dra den gröna, blå respektive orange kulan.

Anta att man drar kulorna en i taget och att de inte läggs tillbaka efter dragning. Vad är sannolikheten att först dra en grön kula och sedan en orange kula?

Som du ser påverkas utfallet vid den andra dragningen av vad som hände vid den första. Till exempel — om den orange kulan dras först, finns det inga orange kulor kvar. Därför är sannolikheten att dra en orange kula vid den andra dragningen 0 i det fallet. När kulorna dras en i taget utan att läggas tillbaka, finns det totalt 6 möjliga utfall för att dra två kulor.
G B & G O B G & B O O G & O B
Av de 6 möjliga utfallen är det bara 1 utfall som motsvarar att först dra den gröna kulan och sedan den orange. Därför är sannolikheten för att detta inträffar 1/6.
P(först G och sedan O)= 1/6
Nästa steg är att beräkna sannolikheten för varje händelse var för sig. Sannolikheten att först dra en grön kula får man genom att dela antalet gynnsamma utfall med det totala antalet kulor. Skålen innehåller totalt 3 kulor, varav 1 är grön.
P( G)= 1/3
Om det är givet att den första dragningen är grön, finns det fortfarande 1 orange kula kvar i skålen. Men nu finns det bara 2 kulor kvar totalt. Därför är sannolikheten att dra den orange kulan, givet att den första var grön, 1/2.
P( Ogiven G)= 1/2
Sammanfattningsvis är händelserna beroende, eftersom den första händelsen påverkar sannolikheten för att den andra inträffar. Detta bekräftas också av regeln för beroende händelser.
P(först G och sedan O) & = P( G) & * & P( Ogivet G) [0.3em] 1/6 & = 1/3 & * & 1/2
Multiplikation av sannolikheter
När man gör flera olika slumpförsök, eller när ett upprepas, får man en kombination av händelser. Sannolikheten för att både händelse A och B, från olika slumpförsök, inträffar får man genom att multiplicera deras individuella sannolikheter.
P(A och B) = P(A) * P(B)
Vad är sannolikheten för två beroende händelser?
Ledtråd
Analysera om händelserna att välja en spader första och andra gången är beroende eller oberoende. Multiplicera sedan deras sannolikheter.
Lösning
Multiplicera bråk
Förkorta med 13
Förkorta med 4
Addition av sannolikheter
För två händelser, A och B, som inte kan inträffa samtidigt, är sannolikheten att någon av dem inträffar summan av deras individuella sannolikheter.
P(AellerB)=P(A)+P(B)
Träddiagram
Ett träddiagram visar alla möjliga utfall i ett slumpförsök som består av flera steg, till exempel att kasta en tärning två gånger. Diagrammet består av noder och grenar som visar varje val eller händelse.
- Noder: Varje nod representerar ett specifikt utfall i försöket.
- Grenar: En gren kopplar ihop två noder. Från varje nod kan det gå flera grenar som visar olika möjliga fortsättningar.
För att skapa ett träddiagram som visar alla möjliga utfall när man kastar en tärning två gånger, börjar man med en rotnod. Från denna nod ritar man en gren för varje möjligt utfall av det första kastet. I slutet av varje gren skapar man en ny nod som representerar resultatet av det kastet.

Oavsett vilket resultat man får vid det första kastet, finns det sex möjliga utfall även vid det andra kastet. Därför ritas sex grenar från varje nod efter det första kastet, som leder till noder för de möjliga utfallen av det andra kastet.

Slutnoderna i träddiagrammet visar alla möjliga utfall i detta experiment — totalt 36 stycken. Sannolikheten att få två ettor när man kastar en tärning två gånger är då 1/36, eftersom det bara finns ett gynnsamt utfall för den händelsen. Detta motsvaras av den allra första grenen i träddiagrammet.
P(1och1)=1/36
Denna sannolikhet kan också beräknas genom att multiplicera sannolikheten för den första händelsen med sannolikheten för den andra. Sannolikheten att slå en etta på kast 1 är 1/6. Samma sannolikhet gäller för att få en etta på kast 2.
P(1)= 1/6
Multiplicera bråk
Denna regel gäller endast när den ena händelsen inte påverkar den andra. Om sannolikheten för händelse A är P(A) och sannolikheten för händelse B är P(B), då är sannolikheten att både A och B inträffar lika med produkten av deras individuella sannolikheter:
P(AochB) = P(A) * P(B)
Träddiagram hjälper till att räkna ut sannolikheter i flerstegsexperiment. Genom att skriva sannolikheter på grenarna ser man hur de kombineras. Om man multiplicerar sannolikheterna längs en gren, kan man snabbt beräkna sannolikheten för ett visst utfall.Beräkna sannolikhet med träddiagram
Två lyckohjul är uppdelade i åtta delar vardera. I det ena hjulet finns siffrorna 1-8 och i det andra finns bokstäverna A–H.

Ledtråd
Bestäm om händelserna är beroende eller oberoende. Hitta deras sannolikheter och beräkna sedan deras produkt.
Lösning
Vi löser uppgiften med ett träddiagram. På första hjulet är 4 av de 8 siffrorna udda, så sannolikheten för att få en udda siffra är P(U)= 4 8 = 12. På andra hjulet är 6 av de 8 bokstäverna konsonanter (B, C, D, F, G och H) så sannolikheten för att hjulet stannar på en sådan är P(K)= 68= 34.

För att beräkna sannolikheten att få både udda siffra och konsonant multipliceras sannolikheterna längs denna väg i träddiagrammet: P(U, K)= 12* 34= 38.
Utfallsmatris

Du kastar två vanliga tärningar.

Vi markerar utfallen där vi får minst en 3:a i ett utfallsrum. Raderna representerar prickarna på den ena tärningen och kolumnerna antalet prickar på den andra.
Av de 36 möjliga utfallen innehåller 11 av dem minst en 3:a. Vi sätter in dessa värden i sannolikhetsformeln.
Vi markerar de utfall där tärningssumman är udda.
Det är 18 gynnsamma utfall och totala antalet utfall är fortfarande 36. Vi sätter in detta i sannolikhetsformeln.
Vi kallar händelsen att ta upp en bok från Henning Mankel för M och händelsen att ta upp en bok från Stieg Larsson för L. Totalt har Oskar 5+3=8 böcker han kan välja mellan. Eftersom fem av dessa är skrivna av Henning Mankel och tre av Steig Larsson blir sannolikheten P(M)=5/8 och P(L)=3/8 att den första boken är skriven av respektive författare. När Oskar tagit den första boken är antalet böcker av den författaren en mindre i bokhyllan och det totala antalet böcker är också en mindre vilket påverkar sannolikheten för vilken författare den andra boken är skriven av. Vi ritar ett träddiagram och markerar händelserna P(H,H) och P(L,L).
Sannolikheten att böckerna är av samma författare är summan av händelserna P(M, M) och P(L, L).
Sannolikheten att båda böcker Oskar tar är från samma författare är alltså ca 46 %.
Minst ett mål innebär att hon sätter en, två eller alla tre straffar. Men beräkningarna blir något lättare om vi istället bestämmer sannolikheten för komplementhändelsen till minst ett mål, nämligen att hon inte gör något mål alls. Om sannolikheten för mål är 40 % är sannolikheten för miss 60 %. Det betyder att P(tre missar)= 0,6 * 0,6 * 0,6=0,216. Om vi kallar händelsen att Petra gör minst ett mål för A, är komplementhändelsen A^c lika med 0,216. För att ta reda på sannolikheten för minst ett mål använder vi sambandet P(A)+P(A^c)=1. Vi sätter in P(A^c) och löser ut P(A).
Sannolikheten är cirka 78 % att Petra gör minst ett mål.
helt säkertatt slå minst en etta om man kastar en tärning femton gånger. Stämmer det verkligen? Motivera med beräkningar.
Vi kallar händelsen att slå minst en etta (dvs. mellan en och femton stycken) för A. Istället för att beräkna sannolikheten för alla kombinationer där man slår minst en etta beräknar vi sannolikheten för komplementhändelsen och subtraherar från 1:
P(A)+P(A^c)=1.
Då sannolikheten att slå en etta när man kastar en tärning är 16 måste sannolikheten för att slå något annat än en etta vara 56. Händelsen A^c är att man slår icke-ettor
i alla kast. Sannolikheten att göra det beräknar vi genom att multiplicera P(inte etta) 15 gånger:
(A^c)=(5/6)^(15)
Nu kan vi beräkna P(A) genom att sätta in P(A^c) i formeln för komplementhändelse.
Sannolikheten är cirka 93,5 % att slå minst en etta så även om sannolikheten är hög att man får minst en etta kan Maximilian inte vara helt säker.
Lyckohjulet ger vinst om det hamnar på ett primtal. Vad är sannolikheten att vinna tre gånger i rad? Svara i hela procent.

Ett primtal är ett heltal större än 1 och som endast är delbart med 1 och sig själv. Hjulet har 6 primtal. 2, 3, 5, 7, 11 och 13. Av 16 möjliga utfall är alltså 6 gynnsamma. Vi sätter in dessa värden i sannolikhetsformeln.
Sannolikheten för att två eller flera påföljande händelser inträffar är produkten av händelsernas sannolikheter.
Sannolikheten att vinna tre gånger i rad är ca 5 %.
Du ska gå genom skogen hem till din kompis men du vet inte vilken väg du ska ta. Hur stor är sannolikheten att du tar rätt väg genom skogen? Svara i hela procent.

Vi antar att det är lika sannolikt att du väljer en stig som en annan när du står vi ett vägskäl. När stigen delar sig i två delar är sannolikheten 12 att man väljer någon av dem och när de finns tre är sannolikheten 13. Då kan vi illustrera sannolikheterna att ta de olika stigarna med ett träddiagram där V står för vänster, H för höger och R för rakt fram.
I diagrammet har vi markerat de två vägar genom skogen som leder fram till huset. Genom att multiplicera sannolikheterna längs dessa två grenar och summera produkterna kan vi beräkna sannolikheten att du tar rätt väg fram genom skogen.
Det är 29 % sannolikhet att du tar rätt väg.
Det kostar 5 kr att delta i ett lotteri. Man plockar då två kulor från urnan och vinner summan av beloppen som står på kulorna. Vad är sannolikheten att man minst får tillbaka det man satsat?

På hur många sätt kan minst få tillbaka det man satsat? Ganska många. T.ex. kan man plocka 10 kr+5kr eller 0 kr + 15 kr. Det blir ganska knöligt att beräkna sannolikheterna för alla kombinationer. Vi undersöker istället komplementhändelsen dvs. att man går med förlust. Det kan man bara göra genom att plocka båda gula kulorna.
Det finns två gula bollar av fem. Sannolikheten för att dra en av dem i första dragningen blir då P(gul)=2/5. Andra gången man drar finns det fyra bollar kvar och en av dessa är röd, vilket ger sannolikheten 14. Den totala sannolikheten för att dra båda röda bollar beräknar vi genom att multiplicera sannolikheterna.
Sannolikheten att gå med förlust är alltså 0,1. Detta är komplementhändelsen till att minst få pengarna tillbaka. Summan av de båda sannolikheterna är 1, vilket betyder att P(minst pengarna tillbaka)=1-0,1=0,9.
En riddare har lyckats fly från sin fängelsehåla och har vakterna hack i häl. Han springer för sitt liv genom fängelset och kan inte vända om och springa tillbaka eftersom han då möter vakterna. Hur stor sannolikhet är det att riddaren blir fri? Svara i hela procent.

Vi illustrerar riddarens flykt med ett träddiagram. Vid första vägskälet kan riddaren välja mellan tre vägar: höger (H), rakt fram (R) eller till vänster (V). Sannolikheten att han väljer rätt väg (rakt fram) är 13.
Om han tar rätt väg ska han svänga höger (ur riddarens perspektiv) vid nästa vägskäl och eftersom han har två valmöjligheter blir sannolikheten 12 att han tar rätt väg. Vi kompletterar ovanstående träddiagram och markerar vägen till frihet i träddiagrammet.
Genom att multiplicera sannolikheterna längs den markerade grenen i träddiagrammet kan vi beräkna sannolikheten att riddaren blir fri.
Det är ca 17 % sannolikhet att riddaren blir fri.
I en skål finns 9 kulor: 3 av dem är vita, en är lila och resten är svarta. Wilhelm tar först en kula och sedan tar Josefin en. Träddiagrammet beskriver sannolikheten för olika utfall.

Besvara frågan och ange alla sannolikheter som bråk.
Det finns bara en lila kula, så det är inte möjligt att båda plockar en sådan. Det enda sättet för dem att ta kulor som har samma färg är om de båda är svarta eller vita. Vi markerar de vägarna i diagrammet.
Sannolikheten för att båda plockar en vit beräknar vi genom att multiplicera sannolikheterna längs den vägen.
Sannolikheten för att båda plockar en svart beräknar vi på samma sätt: P(svart,svart)=5/9*4/8=5/18. För att beräkna sannolikheten att någon av dessa händelser inträffar lägger vi ihop deras sannolikheter.
Sannolikheten att de plockar kulor av samma färg är alltså 1336.
Om Josefin ska plocka en lila kula, får inte Wilhelm plocka den först. Det finns alltså två vägar i träddiagrammet som ger Josefin en lila kula. Antingen om Wilhelm först plockar en svart eller en vit.
Vi beräknar sannolikheten för båda vägar genom att multiplicera sannolikheterna längs med dem: P(vit,lila)=3/9*1/8 och P(svart,lila)=5/9*1/8. Nu summerar vi dessa sannolikheter.
Sannolikheten att Josefin plockar en lila kula är alltså 19.
Johanna har 5 vita och 3 gula golfbollar i sin golfbag. Hon tar upp två bollar ur bagen.
Hur stor är sannolikheten att Johanna får två vita bollar? Svara exakt.
Hur stor är sannolikheten att Johanna får en boll av vardera färgen? Svara exakt.
Johannas situation handlar om ett slumpförsök i flera steg. Hon har 5 vita och 3 gula golfbollar, så hon har totalt 8 bollar. När hon tar upp en första boll är sannolikheten för att den är vit P(vit)=5/8. Om hon fått en vit boll finns det 7 bollar kvar i bagen, varav 4 är vita. Sannolikheten att Johanna på måfå får upp en vit boll till är därför P(vit, om $1$:a vit)=4/7. När man gör flera slumpförsök fås den slutliga sannolikheten av produkten av de enskilda sannolikheterna. Alltså ges sannolikheten för att Johanna får upp två vita bollar av P(två vita)=5/8*4/7. Slutligen beräknar vi denna bråkmultiplikation. Notera att man kan förkorta med 4 eftersom det finns en 4:a i täljaren och en 8:a i nämnaren.
Sannoliheten att Johanna får upp två vita bollar är alltså 514.
Istället för att titta direkt på sannolikheter för att få upp olika färger kan vi beräkna sannolikheten för komplementhändelsen, alltså sannolikheten för att Johanna får upp två bollar av samma färg. Vi har redan beräknat sannolikheten för att få två vita bollar till 514. På samma sätt som i första deluppgfiten beräknar vi sannolikheten för att få två gula bollar.
Sannolikheten för att Johanna först får en gul boll är P(gul)=3/8. Om hon fått en gul boll finns det 2 gula kvar i bagen och sannolikheten att hon får upp en gull boll till är P(gul, om $1$:a gul)=2/7. Den totala sannolikheten för två gula bollar ges av produkten av de enskilda sannolikheterna: P(två gula)=3/8*2/7. Notera att man här kan förkorta med 2 eftersom det finns en 2:a i täljaren och en 8:a i nämnaren. P(två gula)=3/8*2/7 = 3*2/4*2*7= 3/28. Eftersom sannolikheten att få två bollar av samma färg är 514 för vita och 328 för gula så är sannolikheten för att Johanna får upp en boll av varje färg 1 - 5/14 - 3/28 . Detta går förenkla med regler för bråkräkning, men vi tar till miniräknaren direkt och beräknar 1 - 5/14 - 3/28≈ 0,54 = 54 % . Sannolikheten att Johanna får upp två bollar med olika färg är 54 %.
Peter har en påse med 4 röda kulor och 6 vita kulor.
Peter drar slumpmässigt en kula ur påsen. Hur stor är sannolikheten att han får en röd kula?
Peter ställer upp sannolikheten för en händelse som 610* 59. Vilken händelse har han beräknat sannolikheten för?
Peter ställer upp sannolikheten för en händelse som 410* 610. Vilken händelse har han beräknat sannolikheten för?
Det finns totalt 10 st kulor i påsen, vilket innebär att antalet möjliga utfall är 10. Av dessa kulor är 4 st röda, och antalet gynnsamma utfall är därför 4. Vi sätter in detta i formeln för sannolikhet.
Sannolikheten för att dra en röd kula ur påsen är alltså 0.4.
Sannolikheten som Peter har ställt upp är en multiplikation, så vi kan anta att det är två slumpförsök som har sker efter varandra. I nämnaren står antalet möjliga utfall, vilket i det här fallet är antalet bollar. Den sänks från 10 till 9 mellan sannolikheterna, så det dras en boll i första händelsen som inte läggs tillbaka. Vi ritar ett träddiagram med de olika utfallen.
Vi kan nu identifiera de grenarna i trädet som motsvarar sannolikheterna 610 och 59 i uppställningen.
Genom att multiplicera sannolikheterna får man den sammanslagna sannolikheten för vägen, P(vit, vit)=6/10 * 5/9, vilket är det vi söker. Peter har alltså beräknat sannolikheten för att dra två vita kulor efter varandra, utan återläggning.
I deluppgift B hade vi två slumpförsök efter varandra och det har vi nu med. Vi ser dock nu att nämnaren är 10 för båda termerna, så även i den andra dragningen finns det 10 kulor i påsen. Det betyder att den första kulan läggs tillbaka innan den andra dras. Vi ritar upp ett träddiagram som beskriver olika sätt att dra två kulor med återläggning.
Vi markerar den väg som matchar uppställningen, vilket ger den sammanlagda sannolikheten P(röd, vit)= 410 * 610. Peter har alltså beräknat sannolikheten för att först dra en röd kula och sedan en vit kula, med återläggning av den första kulan.
Vid en skidtävling med 20 deltagare sker starten individuellt. Deltagarna ska ha nummerlappar med nummer 1 till 20, där numret anger startordningen.
Marcus och Erik ska delta i tävlingen och båda vill starta sist, det vill säga båda vill ha nummer 20. Innan start får deltagarna slumpmässigt dra ett kuvert som innehåller en nummerlapp. Marcus får dra ett kuvert först av alla och Erik får dra direkt efter.
Innan de öppnar kuverten så säger Marcus till Erik: ”Det är större chans att nummer 20 finns i mitt kuvert än i ditt eftersom jag fick dra först”.
Avgör om Marcus har rätt genom att bestämma sannolikheterna för att Marcus respektive Erik får startnummer 20.
Det finns 20 kuvert och sannolikheten att ett visst kuvert (det man drar) innehåller startnummer 20 är 120 (=5 %). Sannolikheten är samma för Marcus och Erik, det spelar ingen roll vem som drar först!
Är det inte övertygande borde detta argument visa att Marcus inte kan ha större chans än Erik: Antag att alla kuvert delas ut till 20 deltagare. Sannolikheten för var och en av dem att just den personen har fått nr. 20 är 120. Marcus kan inte öka sin chanser genom att vara snabb och öppna sitt kuvert först!
Att Marcus tror att han har störst chans beror kanske på att han tänker så här: Om han får nr. 20 finns ju det kuvertet inte kvar när Erik drar sitt kuvert och då är chansen att han får nr. 20 lika med 0 . Det är sant, men om Marcus inte drar nr. 20 så stiger istället chansen för att Erik drar nr. 20 eftersom han bara har 19 kuvert att välja mellan. För slumpförsök i flera steg multipliceras sannolikheterna och talet 19 visar sig "försvinna" genom förkortning: 19/20*1/19=1/20 .
Sveriges största rovfågel är havsörnen. Uppskattningsvis 70 % av de svenska havsörnarna är ringmärkta. Havsörnar som lever i par håller under hela sin livslängd ihop med samma partner.
Beräkna sannolikheten att ett havsörnspar består av två ringmärkta fåglar.
Beräkna sannolikheten att ett havsörnspar består av en ringmärkt och en omärkt fågel.
Ena parten i paret är ringmärkt med sannolikhet 0.7 eftersom vi i problemformuleringen fått veta att ungefär 70 % av alla örnar är ringmärkta. Den andra parten är också ringmärkt med sannolikhet 0.7. Om vi antar att de två eventuella ringmärkningarna är oberoende av varandra, har vi att sannolikheten att båda är ringmärkta är 0.7* 0.7 = 0.49, då vi ska multiplicera de oberoende händelsernas sannolikheter med varandra. Att vi faktiskt kan anta att ringmärkningarna är oberoende av varandra beror på att när örnarna väljer partner tar de förmodligen inte hänsyn till eventuella ringar på benen.
I denna uppgift behöver vi ta hänsyn till på hur många olika sätt precis en av fåglarna kan vara ringmärkt. Eftersom (om vi antar att paret består av en hona och en hane) honan kan vara märkt och hanen omärkt, samt, honan omärkt och hanen märkt. Alltså,
märkt hona, omärkt hane omärkt hona,
märkt hane.
Med sannolikheten 0.7 att en fågel är märkt fås att sannolikheten för att den inte är märkt, komplementhändelsen, är 1-0.7=0.3. Anledningen är att sannolikheten för en händelse plus sannolikheten för komplementhändelsen alltid är 1. Detta ger oss att den efterfrågade sannolikheten är 0.7 * 0.3_(märkt hona omärkt hane) + 0.3 * 0.7_(omärkt hona märkt hane) = 0.42.
De två tärningarna kan ge många olika utfall, exempelvis 3 och 5 såväl som 2 och 1. Totalt finns det 6* 6 = 36 olika utfall då tärningarna var för sig kan visa prickar på 6 olika sätt. Det vi är intresserade av är summan av antalet prickar som tärningarna visar. För att få lite klarhet gör vi en tabell över de olika utfallen med sina respektive summor.

I tabellen kan vi se att summan 7 förekommer sex gånger, vilket är flest av alla möjliga summor. Det betyder att vi ska gissa på 7 prickar för att ha så stor chans som möjligt att vinna.
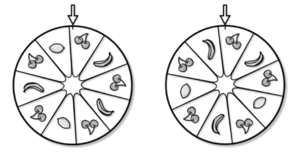
Elin, Petter och Ali är på ett nöjesfält. Där finns ett spel med två likadana snurrande lyckohjul med bilder av bananer, citroner och körsbär. Hjulen snurrar oberoende av varandra. Spelet ger vinst om pilarna på respektive hjul pekar på bilder av samma sorts frukt då hjulen stannar. Se figur.
Elin satsar på att båda hjulen stannar på körsbär. Hur stor är sannolikheten att hon vinner? Svara i procent.
Samtidigt som Elin satsar på körsbär, satsar Petter på bananer och Ali på citroner. Hur stor är sannolikheten att ingen av de tre vinner?
Vardera hjul har 10 fält, varav 5 är körsbär, 3 är bananer och 2 är citroner. Eftersom hälften av fälten är körsbär är sannolikheten för att ett hjul stannar på körsbär 12. När man har flera slumphändelser och man vill ha ett visst utfall för var och en av dessa multipliceras de enskilda sannolikheterna. Sannolikheten att Elin vinner blir därför 1/2*1/2 = 1/4 , vilket är detsamma som 25 %.
När vi ska bestämma vilken sannolikheten är att ingen av Elin, Petter och Ali vinner bestämmer vi först vilken sannolikheten är att någon av dem faktiskt vinner; denna sannolikhet ges av summan av deras olika vinstchanser.
Vi vet redan att Elins chanser till vinst är 25 %.
Petter vinner om båda hjulen stannar på bananer. Sannolikheten att ett hjul stannar på banan är 310 (eftersom det är 3 gynnsamma utfall av 10 möjliga utfall). Sannolikheten för banan på båda hjulen är då 3/10*3/10 = 9/100 , vilket är detsamma som 9 %.
Sannolikheten att Ali vinner beräknas på liknande sett. Citron på ett hjul fås med sannolikheten 210 och sannolikheten att båda hjulen stannar på citron är 2/10*2/10 = 4/100 . eller 4 %.
Vi adderar sannolikheterna för att få sannolikheten för att någon av dem vinner: 25 % + 9 % + 4 % = 38 %. Men det som efterfrågas är vilken sannolikheten är att ingen av dem vinner. Totala sannolikheten är 100 %, den sökta sannolikheten är alltså 100 %-38 %=62 %.