{{ 'ml-label-choose-chapter' | message }} {{ courseTrack.signature }} {{ 'ml-label-choose-course' | message }}

Geometri

Välj kurs
Matte 1a
Geometri
Skala

Skala

{{ 'ml-heading-theory' | message }}

Om man ska rita av något kan det ibland vara oöverskådligt, och i vissa fall omöjligt eller meningslöst, att göra en exakt kopia. Då kan man göra en förminskning eller förstoring. Exempelvis är en karta förminskad jämfört med verkligheten medan en bild på en insekt antagligen är förstorad.

Karta och insekt.jpg
Skala är ett mått på hur mycket man har förminskat eller förstorat. När man talar om skala menar man oftast längdskala, men det finns även area- och volymskala.
Begrepp

Längdskala

En längdskala anger förhållandet mellan längden på en avbildning av ett objekt och objektets verkliga längd. Den kan definieras på följande sätt.

Lngdskalaa¨=Lngd i avbildninga¨Motsvarande lngd i verklighetena¨\text{Längdskala} = \dfrac{\text{Längd i avbildning}}{\text{Motsvarande längd i verkligheten}}

Om längdskalan t.ex. är 14\frac{1}{4} innebär det alltså att avbildningen är en fjärdedel så lång som det verkliga objektet.

Begrepp

Area- och volymskala

Man kan även avgöra hur arean eller volymen i en avbildning förhåller sig till arean eller volymen av det verkliga objektet. Då talar man istället om areaskala respektive volymskala. De definieras på liknande sätt som längdskala.

Areaskala=Area i avbildningMotsvarande area i verkligheten\text{Areaskala} = \dfrac{\text{Area i avbildning}}{\text{Motsvarande area i verkligheten}}

Volymskala=Volym i avbildningMotsvarande volym i verkligheten\text{Volymskala} = \dfrac{\text{Volym i avbildning}}{\text{Motsvarande volym i verkligheten}}


Notation
Skala

Ett vanligt sätt att ange längd-, area- eller volymskala är genom att använda ett kolon. Följande majblomma, som i verkligheten är 44 cm hög, är t.ex. avbildad i längdskalan 1:41:4 vilket betyder samma sak som 14.\frac{1}{4}. Skalan utläses ett till fyra och betyder att 11 cm på bilden motsvarar 44 cm i verkligheten.

förminskad blomma skala 1:4

Generellt gäller det att längden i avbildningen anges till vänster om kolonet och motsvarande längd i verkligheten till höger om kolonet.

Avbildning:Verklighet\text{Avbildning}:\text{Verklighet}

Även för area- och volymskala anges värdena för avbildningen till vänster om kolonet och de verkliga värdena till höger. Om talet till vänster är lägre än det till höger är avbildningen en förminskning medan det är en förstoring om om det vänstra talet är större än det högra.


Uppgift

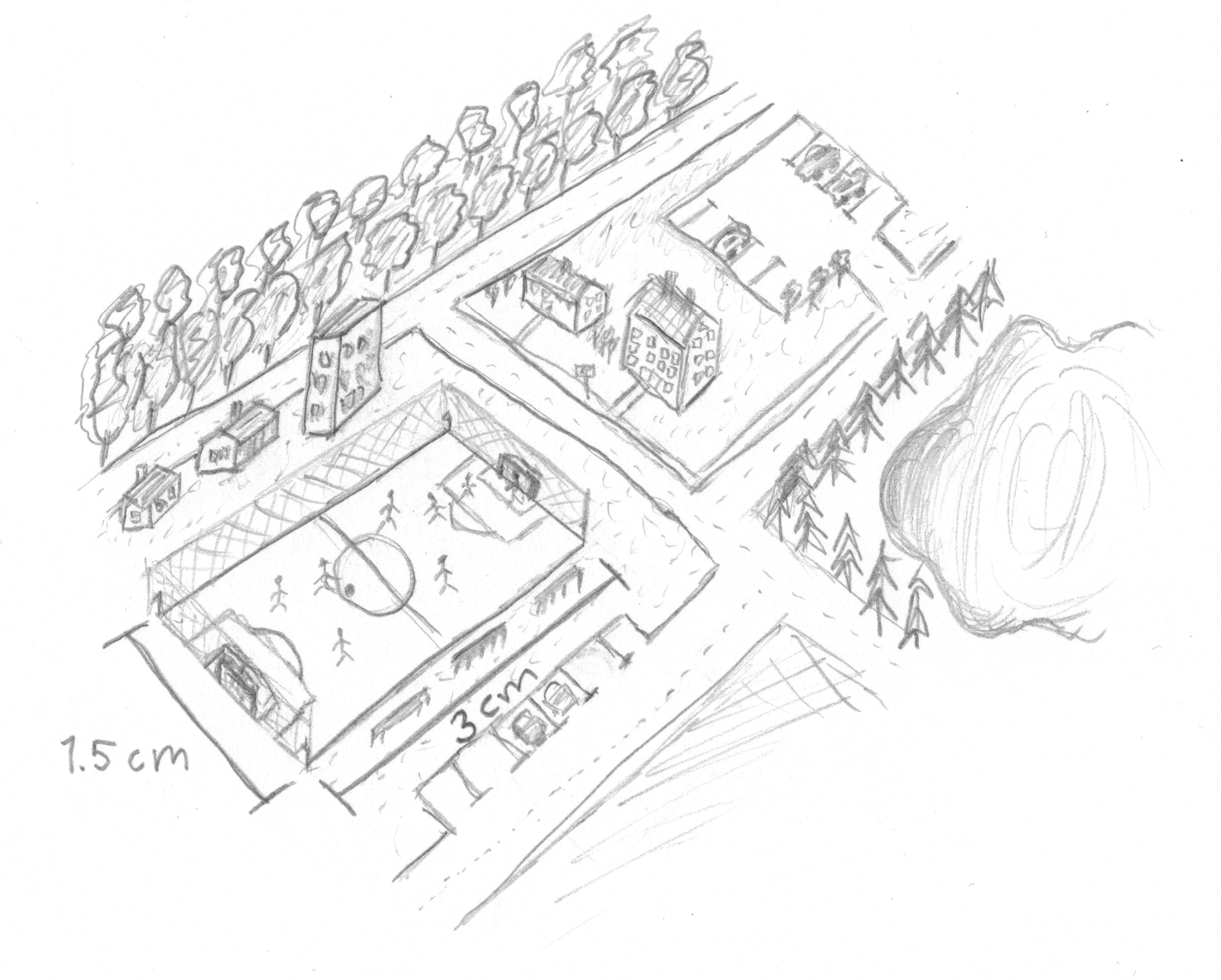
Nike är konstnär och har utmanat sig själv genom att rita av sitt bostadsområde under en helikoptertur.

Helikopterskiss.jpg

Hennes fru är matematiker och har kommit fram till att längdskalan mellan Nikes avbildning och verkligheten är 1:3000.1:3000. Använd denna skala för att bestämma de verkliga längderna på fotbollsplanens sidor.

Lösning

Vi vet att skalan är 1:3000.1:3000. Det betyder att 11 cm på bilden motsvarar 30003000 cm i verkligheten. I skissen ser vi att fotbollsplanens kortsida är 1.51.5 cm och att långsidan är 33 cm. Vi multiplicerar dessa längder med 30003000 för att bestämma hur långa planens sidor är i verkligheten. Kortsida: 1.5⋅3000=4500 cmLngsida:a˚ 3⋅3000=9000 cm\begin{aligned} &\text{Kortsida:}\ 1.5\cdot3000=4500\text{ cm}\\[0.3em] &\text{Långsida:}\ 3\cdot3000=9000\text{ cm} \end{aligned} Till sist skriver vi om längderna till enheten meter, eftersom det är mer användbart i sammanhanget. Det gör vi genom att dividera med 100.100. Vi får då att kortsidan är 4545 m lång och att långsidan är 9090 m lång.

Visa lösning Visa lösning
Uppgift

En röd blodkropp har diametern 88 mikrometer. I en lärobok förstoras en bild på den upp så att diametern blir 44 cm. Vad blir skalan på avbildningen?

Lösning

Vi beräknar skalan genom att dividera längden på avbildningen med den verkliga längden. Men eftersom längderna är i olika enheter måste vi först skriva om dem till samma, t.ex. meter. 11 mikrometer är en miljondels meter vilket betyder att 8 mikrometer=8⋅10-6 m. 8 \ \text{mikrometer} = 8 \cdot 10^{\text{-} 6} \ \text{m}. Det går 100100 cm på en meter så 44 cm är 4100=0.04\frac{4}{100}=0.04 meter. Nu kan vi bestämma skalan.

Skala=Lngd i avbildninga¨Lngd i verklighetena¨\text{Skala}=\dfrac{\text{Längd i avbildning}}{\text{Längd i verkligheten}}
Sätt in värden
Skala=0.048⋅10-6\text{Skala}=\dfrac{0.04}{8 \cdot 10^{\text{-}6}}
Slå in på räknare
Skala=5000\text{Skala}=5000
50005000 kan skrivas som ett bråk med nämnaren 11: 5000=50001. 5000 = \dfrac{5000}{1}. Detta betyder att skalan är 5000 till 1, vilket brukar skrivas 5000:1.\mathbf{5000:1}.
Visa lösning Visa lösning

Uppgifter

Nivå 1
1.1
{{ 'ml-btn-focusmode-tooltip' | message }} settings_overscan

Ange i ord vad följande längdskalor betyder.

a

1:401:40

b

5:15:1

c

3:43:4

1.2
{{ 'ml-btn-focusmode-tooltip' | message }} settings_overscan

Ash har fotograferat följande snöflinga. Vilken bredd har den i verkligheten?

1.3
{{ 'ml-btn-focusmode-tooltip' | message }} settings_overscan

Dragi har en avbildning av kvarteret där han bor. I bilden har han mätt att den kortaste vägen mellan korsningarna Idrottsgatan/Klipparstigen och Yxgatan/Marmeladstigen är 7.57.5 cm. Hur lång är den kortaste vägen mellan dessa korsningar i verkligheten? Svara i meter.

Kvarter.svg
1.4
{{ 'ml-btn-focusmode-tooltip' | message }} settings_overscan

Ett företag har tryckt upp tröjor med sin logotyp.

Tröja med Mathleaks-logga

Grafikern Joe som designade loggan ritade den ursprungligen 33 cm bred. Vad är längdskalan för loggan på tröjan?

1.5
{{ 'ml-btn-focusmode-tooltip' | message }} settings_overscan

Bilden visar Elicias vardagsrumsgolv.

a

Vad är vardagsrummets omkrets i verkligheten? Svara i meter.

b

Hur stor är vardagsrummets area i verkligheten? Svara i kvadratmeter.

Nivå 2
2.1
{{ 'ml-btn-focusmode-tooltip' | message }} settings_overscan

En modell av världens största kryssningsfartyg Gigantor är 120120 mm lång och har avbildats i skalan 1:2750.1:2750. Nästa år planerar man att göra ett nytt ännu större skepp som ska heta Explosion. Hur långt blir Explosion i meter om skalan mellan det och Gigantor är 2:1.2:1.

2.2
{{ 'ml-btn-focusmode-tooltip' | message }} settings_overscan

Adriana har tagit ett foto på en segelbåt som hon vill köpa och har framkallat det i formatet 10 cm×15 cm.10 \text{ cm}\times 15 \text{ cm}.

Inramad-båt.svg

Nu vill hon förstora upp det (och sina drömmar) så att varje sida blir tre gånger så lång. Vad blir areaskalan mellan det nya och gamla fotot?

2.3
{{ 'ml-btn-focusmode-tooltip' | message }} settings_overscan
Bilden visar kroppsmåtten på en barbiedocka. Alla mått utom längden representerar omkretsen av det markerade området.
Barbieskiss.svg
a

Vad skulle motsvarande mått vara för en 165165 cm lång kvinna om hon hade samma proportioner som barbiedockan? Svara i centimeter.

b
Använd följande storlekstabeller för att avgöra vilken klädstorlek som skulle passa kvinnan, baserat på det bröst-, midje- respektive stussmått som bestämdes i föregående deluppgift.

Vad säger detta om det kroppsideal man kan säga ha spridits via barbiedockor?

Nivå 3
3.1
{{ 'ml-btn-focusmode-tooltip' | message }} settings_overscan

Rubelius granne har köpt en bubbelpool av märket Jaguarzzi. Rubelius gillar inte detta och tänker beställa en egen bubbelpool från Jaguarzzi. Han tänker att längdskalan mellan hans och grannens pool måste vara 2:12:1 för att han givetvis är dubbelt så bra som sin granne. På natten smyger han in till grannen och mäter poolens inre radie och höjd till 1.7 m1.7 \text{ m} respektive 1.2 m.1.2 \text{ m.}

a

Hur många liter vatten rymmer grannens pool? Avrunda till hundratal.

b

Hur många gånger mer vatten rymmer Rubelius Jaguarzzi än grannens?

Test
{{ 'mldesktop-selftest-notests' | message }} {{ article.displayTitle }}!
{{ tests.error }}

{{ 'ml-heading-exercise' | message }} {{ focusmode.exercise.exerciseName }}

keyboard_backspace {{ section.title }} keyboard_backspace {{ 'ml-btn-previous' | message }} {{ 'ml-btn-previous-exercise' | message }} {{ 'ml-btn-next-exercise' | message }} keyboard_backspace {{ 'ml-btn-next-exercise' | message }}